VMPS++
Loading...
Searching...
No Matches
Classes | Functions
Tensors

Detailed Description

Data structures which store symmetric tensors. Only symmetry-allowed non zero blocks are stored. Abelian and non Abelian symmetries are possible. The module consists of the following parts:

Classes

struct  Biped< Symmetry, MatrixType_ >
 
struct  Multipede< Nlegs, Symmetry, MatrixType >
 
class  Basis
 
class  Qbasis< Symmetry >
 
struct  SiteOperator< Symmetry, Scalar_ >
 
class  SiteOperatorQ< Symmetry, MatrixType_ >
 

Functions

template<typename Symmetry , typename MatrixType , typename MatrixType2 , typename MpoMatrixType >
void contract_L (const Tripod< Symmetry, MatrixType2 > &Lold, const vector< Biped< Symmetry, MatrixType > > &Abra, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &W, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOp, Tripod< Symmetry, MatrixType2 > &Lnew, bool RANDOMIZE=false, tuple< CONTRACT_LR_MODE, size_t > MODE_input=make_pair(FULL, 0), const std::unordered_map< pair< qarray< Symmetry::Nq >, size_t >, size_t > &basis_order_map={})
 
template<typename Symmetry , typename MatrixType , typename MatrixType2 , typename MpoMatrixType >
void contract_R (const Tripod< Symmetry, MatrixType2 > &Rold, const vector< Biped< Symmetry, MatrixType > > &Abra, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &W, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOp, Tripod< Symmetry, MatrixType2 > &Rnew, bool RANDOMIZE=false, tuple< CONTRACT_LR_MODE, size_t > MODE_input=make_pair(FULL, 0), const std::unordered_map< pair< qarray< Symmetry::Nq >, size_t >, size_t > &basis_order_map={})
 
template<typename Symmetry , typename MatrixType , typename MpoScalar >
void contract_L (const Tripod< Symmetry, MatrixType > &Lold, const vector< Biped< Symmetry, MatrixType > > &Abra, const unordered_map< tuple< size_t, size_t, size_t, qarray< Symmetry::Nq >, qarray< Symmetry::Nq > >, SparseMatrix< MpoScalar > > &V, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOp, Tripod< Symmetry, MatrixType > &Lnew)
 
template<typename Symmetry , typename MatrixType , typename MpoScalar >
void contract_R (const Tripod< Symmetry, MatrixType > &Rold, const vector< Biped< Symmetry, MatrixType > > &Abra, const unordered_map< tuple< size_t, size_t, size_t, qarray< Symmetry::Nq >, qarray< Symmetry::Nq > >, SparseMatrix< MpoScalar > > &V, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOp, Tripod< Symmetry, MatrixType > &Rnew)
 
template<typename Symmetry , typename Scalar , typename MpoMatrixType >
Scalar contract_LR (const Tripod< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > &L, const vector< Biped< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > > &Abra, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &W, const vector< Biped< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > > &Aket, const Tripod< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > &R, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOp)
 
template<typename Symmetry , typename MatrixType , typename MpoMatrixType >
void contract_R (const Tripod< Symmetry, MatrixType > &Rold, const vector< Biped< Symmetry, MatrixType > > &Abra, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &Wbot, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &Wtop, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOpBot, const vector< qarray< Symmetry::Nq > > &qOpTop, Tripod< Symmetry, MatrixType > &Rnew)
 
template<typename Symmetry , typename MatrixType , typename MpoMatrixType >
void contract_L (const Multipede< 4, Symmetry, MatrixType > &Lold, const vector< Biped< Symmetry, MatrixType > > &Abra, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &Wbot, const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &Wtop, const vector< Biped< Symmetry, MatrixType > > &Aket, const vector< qarray< Symmetry::Nq > > &qloc, const vector< qarray< Symmetry::Nq > > &qOpBot, const vector< qarray< Symmetry::Nq > > &qOpTop, Multipede< 4, Symmetry, MatrixType > &Lnew)
 

Function Documentation

◆ contract_L() [1/3]

template<typename Symmetry , typename MatrixType , typename MpoMatrixType >
void contract_L ( const Multipede< 4, Symmetry, MatrixType > &  Lold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  Wbot,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  Wtop,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOpBot,
const vector< qarray< Symmetry::Nq > > &  qOpTop,
Multipede< 4, Symmetry, MatrixType > &  Lnew 
)

Calculates the contraction between a left transfer matrix Lold, two MpsQ tensors Abra, Aket and two MpoQ tensors Wbot, Wtop. Needed, for example, when calculating $\left<H^2\right>$ and no MpoQ represenation of $H^2$ is available.

Definition at line 1439 of file DmrgContractions.h.

◆ contract_L() [2/3]

template<typename Symmetry , typename MatrixType , typename MpoScalar >
void contract_L ( const Tripod< Symmetry, MatrixType > &  Lold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const unordered_map< tuple< size_t, size_t, size_t, qarray< Symmetry::Nq >, qarray< Symmetry::Nq > >, SparseMatrix< MpoScalar > > &  V,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOp,
Tripod< Symmetry, MatrixType > &  Lnew 
)

Contracts a left transfer matrix Lold with two Mps tensors Abra, Aket and a block dependent Mpo tensor V as follows:

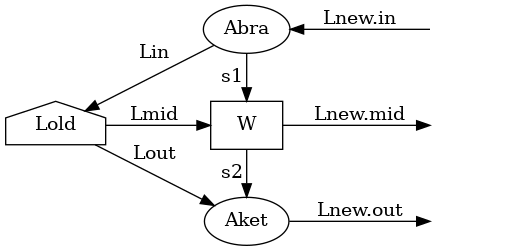
dot_contractQ_L.png

Parameters
Lold
Abra
V
Aket
qloc: local basis
qOp: operator basis
Lnew: new transfer matrix to be written to
Note
This function is used, when the squared Mpo with SU(2) symmetry was precalculated, since in this case the Mpo matrices depend on the symmetry block. For this reason the special member Vsq of the Mpo is used.

Definition at line 328 of file DmrgContractions.h.

◆ contract_L() [3/3]

template<typename Symmetry , typename MatrixType , typename MatrixType2 , typename MpoMatrixType >
void contract_L ( const Tripod< Symmetry, MatrixType2 > &  Lold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  W,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOp,
Tripod< Symmetry, MatrixType2 > &  Lnew,
bool  RANDOMIZE = false,
tuple< CONTRACT_LR_MODE, size_t >  MODE_input = make_pair(FULL,0),
const std::unordered_map< pair< qarray< Symmetry::Nq >, size_t >, size_t > &  basis_order_map = {} 
)

Contracts a left transfer matrix Lold with two MpsQ tensors Abra, Aket and an MpoQ tensor W as follows:

dot_contractQ_L.png

Parameters
Lold
Abra
W
Aket
qloc: local basis
qOp: operator basis
Lnew: new transfer matrix to be written to
RANDOMIZE: if true, set right blocks but fill result with random numbersAA
MODE_input: if FULL, simple contraction, if TRIANGULAR, contract only the lower triangle $a<b$, if FIXED contract with fixed $a$
Note
The quantum number flow for the left environment is $i+a=j$ where $i$ is the index L.out (ket layer), $a$ the index L.mid (MPO layer) and $j$ the index L.in (bra layer). This corresponds to the CGC $C^{i,a\rightarrow j}_{m_i,m_a\rightarrow m_j}$.

Definition at line 35 of file DmrgContractions.h.

◆ contract_LR()

template<typename Symmetry , typename Scalar , typename MpoMatrixType >
Scalar contract_LR ( const Tripod< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > &  L,
const vector< Biped< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > > &  Abra,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  W,
const vector< Biped< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > > &  Aket,
const Tripod< Symmetry, Matrix< Scalar, Dynamic, Dynamic > > &  R,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOp 
)

Calculates the contraction between a left transfer matrix L, two MpsQ tensors Abra, Aket, an MpoQ tensor W and a right transfer matrix R. Not really that much useful.

Parameters
L
Abra
W
Aket
R
qloc: local basis
qOp: operator basis
Returns
: result of contraction
Warning
Not working for non-abelian symmetries.

Definition at line 914 of file DmrgContractions.h.

◆ contract_R() [1/3]

template<typename Symmetry , typename MatrixType , typename MpoScalar >
void contract_R ( const Tripod< Symmetry, MatrixType > &  Rold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const unordered_map< tuple< size_t, size_t, size_t, qarray< Symmetry::Nq >, qarray< Symmetry::Nq > >, SparseMatrix< MpoScalar > > &  V,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOp,
Tripod< Symmetry, MatrixType > &  Rnew 
)

Contracts a right transfer matrix Rold with two Mps tensors Abra, Aket and a block dependent Mpo tensor V as follows:

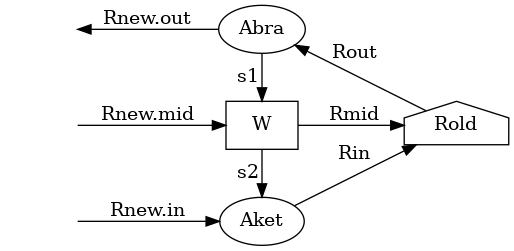
dot_contractQ_R.png

Parameters
Rold
Abra
V
Aket
qloc: local basis
qOp: operator basis
Rnew: new transfer matrix to be written to
Note
This function is used, when the squared Mpo with SU(2) symmetry was precalculated, since in this case the Mpo matrices depend on the symmetry block. For this reason the special member Vsq of the Mpo is used.

Definition at line 433 of file DmrgContractions.h.

◆ contract_R() [2/3]

template<typename Symmetry , typename MatrixType , typename MpoMatrixType >
void contract_R ( const Tripod< Symmetry, MatrixType > &  Rold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  Wbot,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  Wtop,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOpBot,
const vector< qarray< Symmetry::Nq > > &  qOpTop,
Tripod< Symmetry, MatrixType > &  Rnew 
)

Calculates the contraction between a right transfer matrix Rold, two MpsQ tensors Abra, Aket and two MpoQ tensors Wbot, Wtop. Needed, for example, when calculating $\left<H^2\right>$ and no MpoQ represenation of $H^2$ is available.

Definition at line 1279 of file DmrgContractions.h.

◆ contract_R() [3/3]

template<typename Symmetry , typename MatrixType , typename MatrixType2 , typename MpoMatrixType >
void contract_R ( const Tripod< Symmetry, MatrixType2 > &  Rold,
const vector< Biped< Symmetry, MatrixType > > &  Abra,
const vector< vector< vector< Biped< Symmetry, MpoMatrixType > > > > &  W,
const vector< Biped< Symmetry, MatrixType > > &  Aket,
const vector< qarray< Symmetry::Nq > > &  qloc,
const vector< qarray< Symmetry::Nq > > &  qOp,
Tripod< Symmetry, MatrixType2 > &  Rnew,
bool  RANDOMIZE = false,
tuple< CONTRACT_LR_MODE, size_t >  MODE_input = make_pair(FULL,0),
const std::unordered_map< pair< qarray< Symmetry::Nq >, size_t >, size_t > &  basis_order_map = {} 
)

Contracts a right transfer matrix Rold with two Mps tensors Abra, Aket and an Mpo tensor V as follows:

dot_contractQ_R.png

Parameters
Rold
Abra
W
Aket
qloc: local basis
qOp: operator basis
Rnew: new transfer matrix to be written to
RANDOMIZE: if true, set right blocks but fill result with random numbers
MODE_input: if FULL, simple contraction, if TRIANGULAR, contract only the lower triangle $a<b$, if FIXED contract with fixed $a$
Note
The quantum number flow for the right environment is $i+a=j$ where $i$ is the index R.in (ket layer), $a$ the index R.mid (MPO layer) and $j$ the index R.out (bra layer). This corresponds to the CGC $C^{i,a\rightarrow j}_{m_i,m_a\rightarrow m_j}$.

Definition at line 180 of file DmrgContractions.h.